Original URL: https://www.theregister.com/2014/05/29/theorems_5_monte_carlo/
About to make a big bet? Don't crash out, cash in with the power of maths
From biz changes to Monte Carlo, probabilities of risk explained
Posted in On-Prem, 29th May 2014 09:01 GMT
Big Data's Big 5 When and how to make change to a successful business or popular website can be a huge risk. Get things right and - at best - nobody notices. Get things wrong, however, and you run the risk of losing business and suffering a damaged reputation.
A good recent example is that of film and TV service Netflix, whose fluffed introduction of separate DVD and streaming charges in 2011 saw its previously high-flying chief executive Reid Hastings forced into a grovelling apology.
Change can have anticipated as well as unforeseen consequences. Understanding the risk involved is essential. If only there were only some structured way to account for risk in your analysis and decision making...
Happily, there is. Let’s start with a class of problem and then show you a way to solve it.
Take the website change example. You know that your customers fall into five age groups:
- 1-10
- 11-17
- 18-25
- 26-35
- Over 35
They also fall into four classes in terms of how long they have been using the site:
- New and keen
- Old and jaded
- Old and still keen
- Super cool
You have six classes of web page:
- Intro
- Sales
- Maps
- Products
- Information
- Promotion
You also have different classes of advertisements that appeal, in different ways, to the different age groups and classes of users.
You know the numbers of different customer age groups and classifications and also how each combination reacts to your different classes of web pages and advertisements.
You are asked whether the site will make more money if you add more information pages - which the “old and jaded” hate but the “new and keen” love - at the expense of maps that the “super cools” love (even though they would never admit it) but both “old” groups detest.
In other words, you are being asked to predict what effect changing the balance of the web pages classes will have. The “classic” way of solving this type of problem is to calculate how a set of probabilities would interact.
You are probably (he typed hopefully) familiar with the concept of probabilities and how independent variables interact. Suppose that you and I drink at the same watering hole from time to time; you have a 50 per cent chance of being there on Friday night and I a 70 per cent chance. We can calculate the probability of meeting there simply by multiplying the probabilities (expressed, not as percentages, but as values between zero and one), so 0.5 x 0.7 = 0.35 meaning we have a 35 per cent chance of meeting.
We can combine probability calculations with combinatorial ones. Suppose we have a mutual friend, Fred, who has a 20 per cent chance of turning up. There are eight possible combinations of meeting, each with a probability:
| Who | Per cent |
|---|---|
| No one | 12 |
| Me | 28 |
| You | 12 |
| Fred | 3 |
| You and me | 28 |
| You and Fred | 3 |
| Fred and me | 7 |
| All of us | 7 |
| Total | 100 |
The problem is that the number of combinations grows very quickly; ten topers would produce 1,024 combinations. So trying to calculate all the combinations of website customers, pages, advertisements and so on rapidly becomes very tedious. And that’s where another technique becomes useful: the Monte Carlo simulation.
Let’s take a real example (one that you will probably never want to solve yourself!) that illustrates the advantage of a Monte Carlo simulation beautifully and also introduces you to its inventor.
Stanislaw Marcin Ulam was a mathematician who worked on the Manhattan Project in Los Alamos at the invitation of John von Neumann, so we can assume he was reasonably good at difficult sums. In 1946 he was laid up in hospital and bored, so he started playing Canfield Solitaire. He fell to wondering how often it could be expected to "come out."
According to Ulam:
After spending a lot of time trying to estimate them by pure combinatorial calculations, I wondered whether a more practical method than ‘abstract thinking’ might not be to lay it out say one hundred times and simply observe and count the number of successful plays.
This was already possible to envisage with the beginning of the new era of fast computers, and I immediately thought of problems of neutron diffusion and other questions of mathematical physics, and more generally how to change processes described by certain differential equations into an equivalent form interpretable as a succession of random operations. Later [in 1946], I described the idea to John von Neumann, and we began to plan actual calculations.
And there you have the whole concept of Monte Carlo simulations in a nutshell. Here was a problem where performing the necessary calculations defeated a world-class mathematician - but the problem was perfectly amenable to being solved using a Monte Carlo simulation.
The Monte Carlo simulation in this case could be a computer program that simply shuffled (randomised) the cards, laid them out, and then played to the rules. Of course, the next time it played, the order of the cards would be different (because of the randomisation during shuffling), so each game could have a different outcome. All the computer has to do is to play a hundred (or ten thousand) games and count the number of times it came out. At the end of it, we would have a very close approximation to the number we seek.
You... lost in the desert
It is worth noting that a combinatorial approach, were it possible, could actually be considered to produce a proof of the number of times Canfield solitaire comes out. A Monte Carlo simulation is never a proof because it might just happen that, time after time, by random luck, the cards would shuffle to a solvable solution. But the chances are very, very much against that happening. A Monte Carlo simulation, whilst not offering a proof, is often used and does provide a very good estimation very rapidly.
One of the key elements of a Monte Carlo simulation is the randomising part and that makes it a stochastic (as opposed to deterministic) process. A deterministic process produces the same answer every time it is run, assuming that we use the same starting values.
So, 0.5 x 0.7 always gives a 35 per cent chance of meeting in the pub. Stochastic systems/processes on the other hand display a level of indeterminacy. From the same starting point it is possible to reach several (possibly an infinite number) of outcomes. To provide that level of indeterminacy in practice, some of the numbers we use in a Monte Carlo simulation are random.
You are lost in the desert. You take a single step in a random direction. Then you take another, but the direction of the second is entirely random with respect to the first step. The question is, at the end of n steps, how far away are you from the starting point?
So, let’s go back to our website. You could try to solve the problem by assigning a set of probabilities to all the possible outcomes of users interacting with web pages but I really wouldn’t advise doing this. However a Monte Carlo simulation would be relatively simple.
In a computer program we could set up a pool of users. The relative proportions of the different age groups and classes would be representative of the observed users of the website. We could generate a “pool” of web pages in a similar way. Now we pick a user at random from the pool (there’s the indeterminacy) and let them interact with a randomly chosen (indeterminate) web page.
Note that while we choose the user randomly, they are being chosen from a pool where the proportions of the different user types is carefully set to represent reality; so if there are more elderly users of the website, then the chances of selecting one of those is higher. The same applies to the selection of web pages.
“Ah,” you may well be thinking, “but we’d need to track the users as they follow links between pages.” OK, so we build those links into the model. “But users don’t start at ‘random’ pages on a website, some pages are much more likely than others.” OK, so build that into the rules of your model.
So, does it actually work?
Of course, I wouldn’t be wasting your time if it didn’t. Let’s look at a really simple example in action with the Random Walk problem. You are lost in the desert. You take a single step in a random direction. Then you take another, but the direction of the second is entirely random with respect to the first step.
The question is, at the end of n steps, how far away are you from the starting point? (This problem sounds totally pointless but early last century it was a crucial question – not about people lost in deserts, but about how atoms and molecules move.) The problem was solved mathematically at the time. When I tell you that Einstein worked on it, you get some idea that it is a non-trivial question.
Nowadays we can solve it really easily using a Monte Carlo simulation. We simply write a program that generates random directions and walks the current person (or atom) one step at a time. We can record how far they have got after one step, two steps, three and so on. We do that for 20 people and take the average value for each number of steps.
Finally we plot the averages for each step.
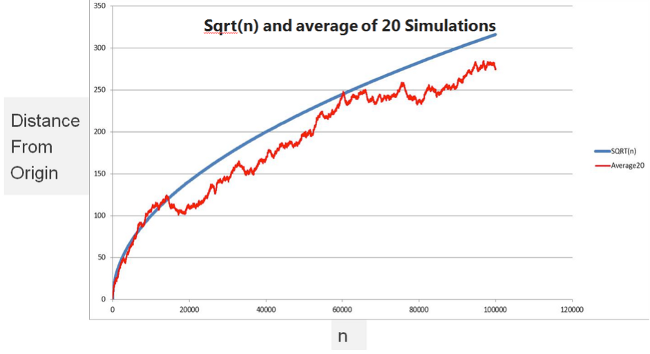
In the chart above you can see the result of 20 simulations for between one and 100,000 steps. The blue line is the square root of (n) and you can see that in this simulation, the two approximate to the same answer. Why stop at 20 simulations; isn’t that what CPU cycles are for?
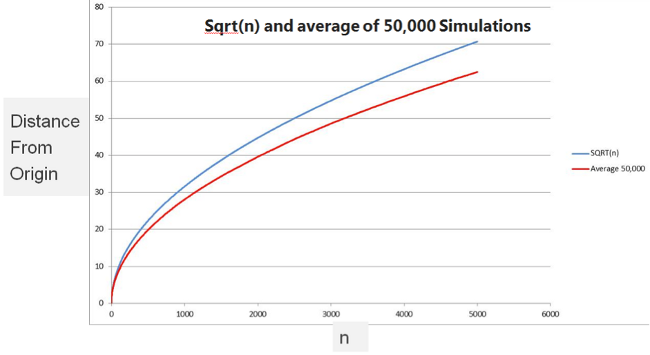
Now, in the above chart, you can see the result of 50,000 simulations for between one and 5,000 steps.
Great mathematicians worked on the random walk problem. It is unlikely that you will be able to get someone of Einstein’s calibre to prove whether a change to your web page is beneficial or not. In practice, you probably don’t need a proof; you just need a very, very good estimation. It would be wise, therefore, to count Monte Carlo simulation amongst your friends. ®