Original URL: https://www.theregister.com/2014/05/20/german_tank_problem_and_leaky_data/
Achtung! Use maths to smash the German tank problem – and your rival
Leaky data is a double agent in intelligence analysis
Posted in Software, 20th May 2014 09:01 GMT
Big Data's Big 5 You've employed Benford's Law to out fraudsters hidden in seemingly random numbers. Now what do you do if you need answers but some of your data is missing? Welcome to the German tank problem, the second in The Reg's guide to crafty techniques from the world of mathematics that can help you quickly solve niggling data problems.
The German Tank problem (and its solution) can allow you to estimate data that you don’t have in order to gain information that you want. A more formal statement of this process is: “The estimation of the maximum of a discrete uniform distribution by sampling (without replacement).” The less formal title, though, is snappier and gives a huge clue as to the provenance.
During the Second World War, the British became very interested in the number of tanks the Germans were producing. Intelligence sources suggested the production was about 1,000 to 1,500 tanks per month. In practice it was nowhere near that high and the wily British boffins found another much more accurate way of estimating production.
They got the squaddies on the battlefield to examine as many captured/disabled tanks as they could and collect all the serial numbers they could find. (In truth this must have been highly exasperating for the soldiers, who probably felt that knocking the tank out in the first place was good enough)
Let’s assume for a moment that tank serial numbers are simple. They all have numbers taken from the same series; the series starts at “1” and increments by one for each new tank.
If we find a tank with the serial number 24 then the Germans have produced at least 24 tanks. However we can be a bit smarter than that. Suppose we see the following numbers: 23, 16, 24, 17, 11, 6, 7, 9 and 12.
That’s nine numbers between seven and 24. If there were actually 4,000 tanks out there, it would seem highly unlikely that our sample would just happen to come from the first 24 produced. It is much more likely that there are only about 30-40 tanks in all out there. (To put that slightly more formally, it is likely that the entire population from which we have drawn our sample is around 30-40.)
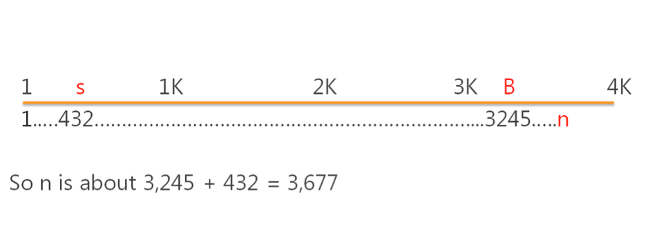
And we can be even smarter. Suppose we examine five tanks (we’ll call the number of examined tanks E, so E=5) with serial numbers of: 432, 3245, 2187, 435, 1542.
The biggest serial number (which we’ll call B) is 3,245, and the smallest (s) is 432. We could reasonably expect as many ‘hidden’ numbers – serial numbers we guess must be out there but for which we have no data – above 3,245 as there are below 432.
In our nomenclature, n is our estimate of the number of tanks.
To put that graphically:
And to put it mathematically:
we hypothesised that (n-B) is roughly equal to (s-1), so if:
n-B = s-1
then we can say that: n=B+(s-1)
which we can solve for n by slotting in the actual numbers.
In our case B=3,245, s=432, n=number of tanks produced, so:
n= 3,245 + (432-1) = 3,676
This is merely one formula for estimating the maximum of a discrete uniform distribution by sampling (without replacement). We can also use:
n = (1+1/E)*B
E, if you remember, is the number of tanks examined, which was five, so:
n = (1 +1/5)*3,245 = 3,894
This particular formula was proposed (PDF) by Roger Johnson of Carleton College in Northfield, Minnesota in the journal Teaching Statistics, Volume 16, Number 2, Summer 1994
You might also wish to try a Bayesian approach. I have no particular axe to grind here. I don’t mind how you do it; the important point is that you can.
Now, as it happens, there are several over-simplifications in my original description, both in the reality of WWII and also if we were trying to solve the same kind of problem today.
Leaky data spills your secrets
For a start, not all tanks may have serial numbers drawn from the same pool – different makes and even marks of tanks may use different sequences of numbers. They may not start at one.
Then there is the problem of random (or not) sampling. Older tanks might be sent to Africa and, if we are disabling more tanks there, then the sample will be biased towards the lower end of the population. And so on.
But that’s OK, it is possible to compensate for these factors. We can check to see if different makes of tank share serial numbers (if any do then we know there are multiple series), we can look at the geographical distribution of serial numbers, identify the more modern marks of the same tank and so on. We can also apply simple logic. The serial number of the engine of my first motorbike was CB450E 1008841. Logic tells me that a production run of 8,841 is more likely than 1,008,841 so I would guess that the bike maker, Honda, started the serial numbers at 1,000,000 rather than 1.
And in practice, there are certain factors in the real example that helped considerably. It turned out that the German tanks had different serial numbers on different components; the gear box numbers were the most helpful, but all contributed to the overall picture.
And it worked. As an example, in June 1941, intelligence suggested tank production was 1,550; the estimate from serial numbers was 244. The actual value (verified after the war) was 271.
In essence the Germans were unwittingly "publishing" a set of data; we could say that they had a data “leak.” That data could be extrapolated to yield valuable information that the Germans certainly did not wish to disclose. All that was required was some early data science work by the boffins of the day.
What resonance does that have for us 70 years later in a much more data-savvy world?
I would argue that there is “leaky” data all around us; all we have to do is to think outside the box. Companies very often don’t think about the data they publish and we can either extrapolate from that data (as in the German Tank problem) or simply extract useful information from it.
For example, it is rumoured that a store in America has commissioned frequent aerial photographs of its competitor’s parking lot; it counts the cars and uses this to estimate footfall. There are also opportunities where the leaked data itself is innocuous but yields valuable information when combined with another set.
So, why is this worth thinking about?
First, your career. Now that you know it is possible, all you have to do is to get used to spotting leaked data – once you are sensitised to it you will find it all around you. Your competitors' websites can be a valuable hunting ground. Think about whether you can use it to estimate some missing data (as with the serial numbers) and/or combine that data with other, seemingly innocuous, sets to produce some vital information. If that information gives your company a commercial advantage then you deserve a bonus and a promotion.
Another reason to look at this is to ponder whether your own company is leaking data in some way that could be turned into useful information by the opposition. If so, plug the hole. You are far less likely to be promoted for this but at least you should get some credit.
Finally, if all else fails, send in the tanks. ®