Original URL: https://www.theregister.com/2013/07/18/data_storage_technology/
Why data storage technology is pretty much PERFECT
There's nothing to be done here... at least on the error-correction front
Posted in Storage, 18th July 2013 08:03 GMT
Feature Reliable data storage is central to IT and therefore to modern life. We take it for granted, but what lies beneath? Digital video guru and IT author John Watkinson gets into the details of how it works together and serves us today, as well as what might happen in the future. Brain cells at the ready? This is gonna hurt.
Digital computers work on binary because the minimal number of states 0 and 1 are easiest to tell apart when represented by two different voltages.
In a flash memory, we can store those voltages directly using a clump of carefully insulated electrons. But in all other storage devices, physical analogs are needed.
In tape or hard disk, for example, we look at the direction of magnetisation, N-S or S-N, in a small area. In an optical disc, the difference is represented by the presence or absence of a small pit.
The very blueprint of our biology, DNA, is a data recording based on chemicals that exist in discrete states. "Bit" errors cause mutations that allow evolution, or result in the missing or malformed proteins, which lead to disease. Data recording is essential to all life.

Data storage everywhere: CD, DVD, DAT, DCC, HDD, MiniDisc, SSD, SD, Sim, floppy disk, SuperDisk, magnetic stripe, barcode
Click for a larger image
A binary medium neither knows nor cares what the data represents. Once we can reliably record binary data then we can record audio, video, still pictures, text, CAD files and computer programs on the same medium and we can copy them without loss.
The only difference between these types of data is that some need to be reproduced with a specific time base.
Timing, reliability, durability and cost...
Different storage media have different characteristics and no single medium is the best in all respects. Hard drives are best at intense read/write applications, but the disk can’t be removed from the drive. And although the recording density of optical discs has been exceeded by hard drives, you can swap out an optical disc in a matter of seconds. Also, because they can be stamped at low cost, they are good for mass distribution.
Flash memory offers rapid access and is rugged and compact, but it is limited in the number of write cycles it can sustain. And even though flash memory wiped out the floppy disk in PCs, floppy disk technology is alive and well. It's in magnetic stripes on airline and rail tickets, on credit cards and hotel room keys. Sometimes a sledgehammer isn’t the right tool and the humble barcode is a perfect example.
In flash memory, the storage density is determined by how finely the individual charge wells can be fabricated. But the same advances in optics that allow smaller and smaller details to be photo-etched on a chip also allow optical discs to resolve smaller and smaller bits.

Flash chip inside USB thumb drive: no moving parts but degenerates with use
In a rotating memory - a spinning disc, whether magnetic or optical - the problem is two-dimensional: we need to pack in as many tracks as possible side by side and we need to pack as many bits into a given length of track as possible.
The tracks are incredibly narrow and active tracking servo systems are needed to keep the heads registered despite tolerances and temperature changes. To eliminate wear there is no contact between the pickup head and the disc.
Optical discs peer at the tracks though a microscope whereas in magnetic drives, the heads "fly" on an air film just nanometres above the disk's surface. Paradoxically, it is flash memory, which has no moving parts, that has the wear mechanism.
Channel coding
Discs scan their tracks and pick up data serially. We can’t just write raw data on the disc tracks, because if that data contained a run of identical bits there would be nothing to separate the bits and the reader would lose synchronism. Instead the data is modified by a process called channel coding. One of channel coding's functions is to guarantee clock content in the signal irrespective of the actual data patterns.
In optical discs the tracking and focusing is performed by looking at the symmetry of the data track through the pickup lens after filtering out the data. A second function of the channel coding is to eliminate DC and low frequency content from the data track so that filtering is more effective. The round light spot finds it hard to resolve events on the track that are too close together.
Mass media

The first mass-produced application of error correction was in the compact disc, launched in 1982, 22 years after the publication of Reed and Solomon’s paper. The optical technology of CD is that of the earlier LaserVision discs, so what was the hold-up?
Firstly, a digital audio disc has to play in real time. The player can’t think about the error like a computer can, but has to correct on the fly. Secondly, if the CD used a simpler system than Reed-Solomon coding, it would have needed to be much larger - hence closing the portable and car player markets to its makers. Thirdly, a Reed-Solomon error-correction system is complex and can only economically be implemented on an LSI chip.
Essentially all of the intellectual property that was needed to make a Compact Disc was already in place a decade earlier, but it was not until the performance of LSI Logic Corp's chips had crossed a certain threshold that it suddenly became economically viable and arrived with a wallop.
By a similar argument, we would later see the DVD emerge only once LSI technology made it possible to perform MPEG decoding in real time at consumer prices.
Joining the dots
The technique used in all optical discs to overcome these problems is called group coding. To give an example, if all possible combinations of 14 bits (16,384 of them) are serialised and drawn as waveforms, it is possible to choose ones that record easily.
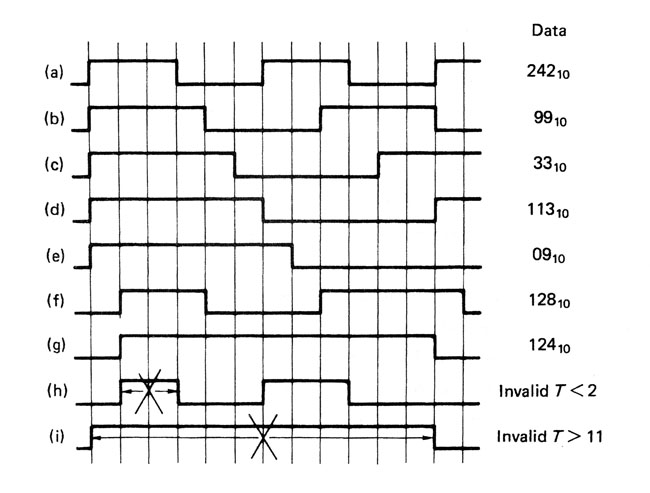
How a group code limits the frequencies in a recording. At a) the highest frequency, transitions are 3 channel bits apart. This triples the recording density of the channel bits. Note that h) is an invalid code. The longest run of channel bits is at g) and i) is an invalid code.
The figure above shows that we eliminate patterns that have changes too close together so that the highest frequency to be recorded is reduced by a factor of three.
We also eliminate patterns that have a large difference between the number of ones and zeros, since that gives us an unwanted DC offset. The 267 remaining patterns that don’t break our rules are slightly greater in number than the 256 combinations needed to record eight data bits, with a few unique patterns left over for synchronising.
EFM - Clever stuff
Kees Immink’s data-encoding technique uses selected patterns of 14 channel bits to record eight data bits - hence its name, EFM (eight-to-fourteen modulation). Three merging bits are placed between groups to prevent rule violations at the boundaries, so, effectively, 17 (14+3) channel bits are recorded for each data byte. This appears counter-intuitive, until you realise that the coding rules triple the recording density of the channel bits. So we win by 3 x 8/17, which is 1.41, the density ratio.
Just the channel coding scheme alone increases the playing time by 41 per cent. I thought that was clever 30 years ago and I still do.
Compact discs and MiniDiscs use the EFM technique using 780 nm wavelength lasers. DVDs use a variation on the same theme called EFM+, with the wavelength reduced to 650 nm.
The Blu-Ray disc format, meanwhile, uses group coding but not EFM. Its channel modulation, called 1,7 PP modulation, has a slightly inferior density ratio but the storage density is increased using a shorter wavelength laser of only 405 nm. The laser isn’t actually blue*. That’s just marketing - a form of communication that doesn’t attempt error-correction or concealment. They just make it up.
Magnetic recorders have heads with two poles like a tiny horseshoe, so when they scan the track, the finite distance between the two poles causes an aperture effect.
The figure shows that the frequency response is that of a comb filter with periodic nulls. Conventional magnetic recording is restricted to the part of the band below the first null, but there is a technique called partial response that operates on energy between the first and second nulls, effectively doubling the data capacity along the track.
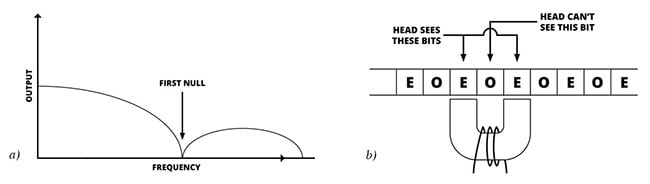
All magnetic recorders suffer from a null in the playback signal a) caused by the head gap. In partial response shown at b), one bit (on odd one) is invisible to the head, which plays back the sum of the even bits either side. One bit later, the sum of two odd bits is recovered.
If it is imagined that the data bits are so small that one of them, let’s say an odd-numbered bit, is actually in the head gap, the head poles can only see the even-numbered bits either side of the one in the middle and produce an output that is the sum of both. The addition of two bits results in a three-level signal. The head is alternately reproducing the interleaved odd and even bit streams.
Using suitable channel coding of the two streams, the outer levels in a given stream can be made to alternate, so they are more predictable and the reader can use that predictability to make the data more reliable. That is the basis of partial-response maximum-likelihood coding (PRML) that gives today’s hard drives such fantastic capacity.
Error correction
In the real world there is always going to be noise due to things like thermal activity or radio interference that disturbs our recording. Clearly the minimal number of states of a binary recording is the hardest to disturb and most resistant to noise. Equally if a bit is disturbed, the change is total, because a 1 becomes a 0 or vice versa. Such obvious changes are readily detected by error correction systems. In binary, if a bit is known to be incorrect, then it is only necessary to set it to the opposite state and it will be correct. Thus error correction in binary is trivial and the real difficulty is in determining which bit(s) are incorrect.
A storage device using binary – and having an effective error correction/data integrity system – essentially reproduces the same data that was recorded. In other words, the quality of the data is essentially transparent because it has been decoupled from the quality of the medium.
Using error correction, we can also record on any type of medium, including media that were not optimised for data recording, such as a pack of frozen peas or a railway ticket. In the case of barcode readers, where the product is only placed in the general vicinity of the reader, the error correction has an additional task to perform: to establish that it has in fact found the barcode.
Once it is accepted that error correction is necessary, we can make it earn its keep. There is obvious market pressure to reduce the cost of data storage, and this means packing more bits into a given space.
No medium is perfect, all contain physical defects. As the data bits get smaller, the defects get bigger in comparison, so the probability that the defects will cause bit errors goes up. As the bits get smaller still, the defects will cause groups of bits, called bursts, to be in error.
Error correction requires the addition of check bits to the actual data, so it might be thought that it makes recording less efficient because these check bits take up space. Nothing could be further from the truth. In fact the addition of a few per cent extra check bits may allow the recording density to be doubled, so there is a net gain in storage capacity.
Once that is understood it will be seen that error correction is a vitally important enabling technology that is as essential to society as running water and drainage, yet is possibly even more taken for granted.
*It's violet
Doing the sums
The first practical error-correcting code was that of Richard Hamming in 1950 (PDF). The Reed-Solomon codes were published in 1960. Extraordinarily, the entire history of error correction was essentially condensed into a single decade.
Error correction works by adding check bits to the actual message, prior to recording, calculated from that message. They are calculated in such a way that no matter what the message itself, the message plus the check bits forms a code word, which means it possesses some testable characteristic, such as dividing by a certain mathematical expression always giving a remainder of zero. The player simply tests for that characteristic and if it is found, the data is assumed to be error-free.

Reed-Solomon Polynomial Codes over Certain Finite Fields paper
Click to view document [PDF]
If there is an error, the testable characteristic will not be obtained. The remainder will not be zero, but will be a bit pattern called a syndrome. The error is corrected by analysing the syndrome.
In the Reed-Solomon codes there are pairs of different mathematical expressions used to calculate pairs of check symbols. An error causes two syndromes. By solving two simultaneous equations it is possible to find the unique location of the error and the unique bit pattern of the error that resulted in those syndromes. A more detailed explanation and worked examples can be found in The Art of Digital Audio.
All present and correct
Without the combination of reliability and storage density it allows, the things we use every day simply wouldn’t work. The images from our digital cameras would be ruined by spots that would make us prefer the grain of traditional film. Our hi-fi would emit gunshots making the crackles of vinyl infinitely preferable and the supermarket barcode reader would mistake the lady in the tweed coat for a tin of baked beans. And whether you could call flash cards or discs compact if they were a metre across is another issue.

How "compact" optical media might have emerged without Reed-Solomon error correction
With the help of error correction, recording densities will keep increasing until fundamental limits are reached. The flash memory using one electron per bit; the disk where one magnetised molecule represents a bit; the optical disc that uses ultra short wavelength light. Maybe it would be called Gamma-Ray. Or a quarkcorder called Murray. More likely storage capacities would level out before those limits are reached. When storage costs are negligible there is no point in making them more negligible.
Making do with perfection
Information theory, first outlined on a scientific basis by Claude Shannon, determines theoretical limits to the correcting power of a system in the same way that the laws of thermodynamics place a limit on the efficiency of heat engines.
However, in the real world, no machines reach the theoretical efficiency limit. Yet the Reed-Solomon error-correcting codes actually operate at the theoretical limit set by information theory. No more powerful code can ever be devised and further research is pointless.
The degree of perfection achieved by error-correction systems is remarkable even by the standards of technology. I suspect this is because the theory of error correction is so specialised and arcane that politicians and beancounters have either never heard of it or daren’t mess with it and it is left to people who know what they are doing.
In contrast, anyone can understand water flowing in a pipe and that is why our drinking water system is in such a shambles - with much of it running to waste through leaks.
Although the coding limits of error correction have been reached, that does not mean that no progress is possible. Error correction and channel coding both require processing power to encode and decode the information and that processing power follows Moore’s Law.
Thus the cost and size of a coding system both diminish with time, or the complexity can increase, making new applications possible. However, if some new binary data storage device is invented in the future using a medium that we are presently not aware of, the error correction will still be based on Reed-Solomon coding. ®
John Watkinson is a member of the British Computer Society and a Chartered Information Technology Professional. He is also an international consultant on digital imaging and the author of numerous books regarded as industry bibles.