This article is more than 1 year old
Why data storage technology is pretty much PERFECT
There's nothing to be done here... at least on the error-correction front
Joining the dots
The technique used in all optical discs to overcome these problems is called group coding. To give an example, if all possible combinations of 14 bits (16,384 of them) are serialised and drawn as waveforms, it is possible to choose ones that record easily.
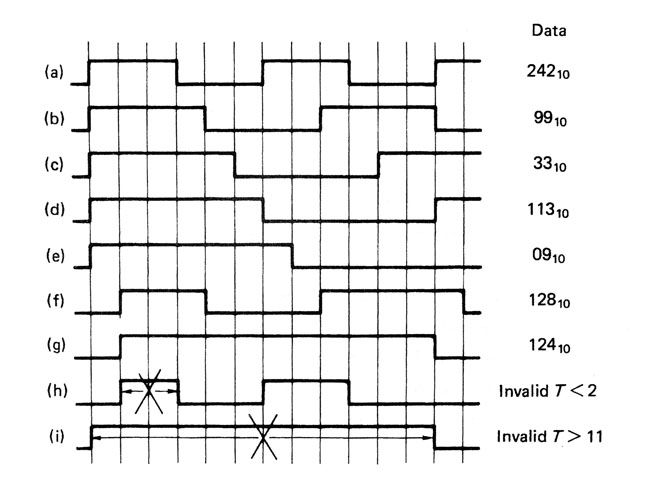
How a group code limits the frequencies in a recording. At a) the highest frequency, transitions are 3 channel bits apart. This triples the recording density of the channel bits. Note that h) is an invalid code. The longest run of channel bits is at g) and i) is an invalid code.
The figure above shows that we eliminate patterns that have changes too close together so that the highest frequency to be recorded is reduced by a factor of three.
We also eliminate patterns that have a large difference between the number of ones and zeros, since that gives us an unwanted DC offset. The 267 remaining patterns that don’t break our rules are slightly greater in number than the 256 combinations needed to record eight data bits, with a few unique patterns left over for synchronising.
EFM - Clever stuff
Kees Immink’s data-encoding technique uses selected patterns of 14 channel bits to record eight data bits - hence its name, EFM (eight-to-fourteen modulation). Three merging bits are placed between groups to prevent rule violations at the boundaries, so, effectively, 17 (14+3) channel bits are recorded for each data byte. This appears counter-intuitive, until you realise that the coding rules triple the recording density of the channel bits. So we win by 3 x 8/17, which is 1.41, the density ratio.
Just the channel coding scheme alone increases the playing time by 41 per cent. I thought that was clever 30 years ago and I still do.
Compact discs and MiniDiscs use the EFM technique using 780 nm wavelength lasers. DVDs use a variation on the same theme called EFM+, with the wavelength reduced to 650 nm.
The Blu-Ray disc format, meanwhile, uses group coding but not EFM. Its channel modulation, called 1,7 PP modulation, has a slightly inferior density ratio but the storage density is increased using a shorter wavelength laser of only 405 nm. The laser isn’t actually blue*. That’s just marketing - a form of communication that doesn’t attempt error-correction or concealment. They just make it up.
Magnetic recorders have heads with two poles like a tiny horseshoe, so when they scan the track, the finite distance between the two poles causes an aperture effect.
The figure shows that the frequency response is that of a comb filter with periodic nulls. Conventional magnetic recording is restricted to the part of the band below the first null, but there is a technique called partial response that operates on energy between the first and second nulls, effectively doubling the data capacity along the track.
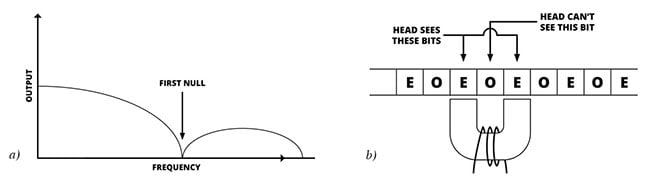
All magnetic recorders suffer from a null in the playback signal a) caused by the head gap. In partial response shown at b), one bit (on odd one) is invisible to the head, which plays back the sum of the even bits either side. One bit later, the sum of two odd bits is recovered.
If it is imagined that the data bits are so small that one of them, let’s say an odd-numbered bit, is actually in the head gap, the head poles can only see the even-numbered bits either side of the one in the middle and produce an output that is the sum of both. The addition of two bits results in a three-level signal. The head is alternately reproducing the interleaved odd and even bit streams.
Using suitable channel coding of the two streams, the outer levels in a given stream can be made to alternate, so they are more predictable and the reader can use that predictability to make the data more reliable. That is the basis of partial-response maximum-likelihood coding (PRML) that gives today’s hard drives such fantastic capacity.
Error correction
In the real world there is always going to be noise due to things like thermal activity or radio interference that disturbs our recording. Clearly the minimal number of states of a binary recording is the hardest to disturb and most resistant to noise. Equally if a bit is disturbed, the change is total, because a 1 becomes a 0 or vice versa. Such obvious changes are readily detected by error correction systems. In binary, if a bit is known to be incorrect, then it is only necessary to set it to the opposite state and it will be correct. Thus error correction in binary is trivial and the real difficulty is in determining which bit(s) are incorrect.
A storage device using binary – and having an effective error correction/data integrity system – essentially reproduces the same data that was recorded. In other words, the quality of the data is essentially transparent because it has been decoupled from the quality of the medium.
Using error correction, we can also record on any type of medium, including media that were not optimised for data recording, such as a pack of frozen peas or a railway ticket. In the case of barcode readers, where the product is only placed in the general vicinity of the reader, the error correction has an additional task to perform: to establish that it has in fact found the barcode.
Once it is accepted that error correction is necessary, we can make it earn its keep. There is obvious market pressure to reduce the cost of data storage, and this means packing more bits into a given space.
No medium is perfect, all contain physical defects. As the data bits get smaller, the defects get bigger in comparison, so the probability that the defects will cause bit errors goes up. As the bits get smaller still, the defects will cause groups of bits, called bursts, to be in error.
Error correction requires the addition of check bits to the actual data, so it might be thought that it makes recording less efficient because these check bits take up space. Nothing could be further from the truth. In fact the addition of a few per cent extra check bits may allow the recording density to be doubled, so there is a net gain in storage capacity.
Once that is understood it will be seen that error correction is a vitally important enabling technology that is as essential to society as running water and drainage, yet is possibly even more taken for granted.
*It's violet
Doing the sums
The first practical error-correcting code was that of Richard Hamming in 1950 (PDF). The Reed-Solomon codes were published in 1960. Extraordinarily, the entire history of error correction was essentially condensed into a single decade.
Error correction works by adding check bits to the actual message, prior to recording, calculated from that message. They are calculated in such a way that no matter what the message itself, the message plus the check bits forms a code word, which means it possesses some testable characteristic, such as dividing by a certain mathematical expression always giving a remainder of zero. The player simply tests for that characteristic and if it is found, the data is assumed to be error-free.

Reed-Solomon Polynomial Codes over Certain Finite Fields paper
Click to view document [PDF]
If there is an error, the testable characteristic will not be obtained. The remainder will not be zero, but will be a bit pattern called a syndrome. The error is corrected by analysing the syndrome.
In the Reed-Solomon codes there are pairs of different mathematical expressions used to calculate pairs of check symbols. An error causes two syndromes. By solving two simultaneous equations it is possible to find the unique location of the error and the unique bit pattern of the error that resulted in those syndromes. A more detailed explanation and worked examples can be found in The Art of Digital Audio.
